Электронные состояния в неупорядоченных системах
Расчет электронных состояний в неупорядоченных средах связан с вычислением статистической суммы
| (8.1) |  |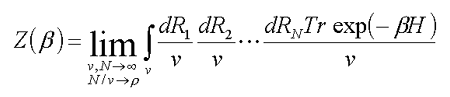
где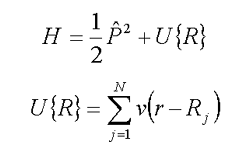 
где Rj – положения примеси, хаотично распределенной по кристаллу.
Основная проблема в вычислении статистической суммы (8.1) – это большая размерность интегрирования, что затрудняет проведение численных расчётов для реальных систем даже на суперкомпьютере. Основная идея исследования уравнения (8.1) заключается в редуцированном описании неупорядоченной системы с помощью корреляционных функций. В качестве таких функций могут быть использованы корреляционные функции плотности среды. Для большого класса сред (жидкости, спиновые стекла, расплавы полимеров, полимерные глобулы) эти функции хорошо численно изучены. Используя идею самосогласованности состояния среды и электрона, для электронной волновой функции можно получить дифференциальное нелинейное уравнение типа Шредингера с эффективным потенциалом V(f,w,Х1,Х2,…), зависящим от волновой функции f, парного потенциала взаимодействия V и корреляционных функций среды Х1,Х2,… :
| (8.2) |  |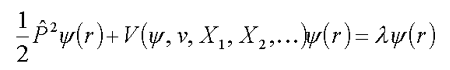
Это уравнение позволяет проводить расчеты электронного состояния в сложной среде с учетом молекулярной структуры среда и ее термодинамического состояния. Образующиеся состояния электрона в полярных средах по своей сути аналогичны полярону. В настоящее время разрабатывается теория, позволяющая проводить расчеты эффективного потенциала, спектра поглощения, эффективной массы и подвижности для поляроноподобных состояний в неупорядоченной среде.
В случае полярных сил взаимодействия и однородной среды это уравнение сводится к уравнению типа (3.2) В случае короткодействующего потенциала и однородной среды v(r-R)=2pas(r-R) минимизация свободной энергии, отвечающей статсумме (8.1), приводит к дифференциальному уравнению вида (приведено по : R.Friedberg, J.M.Luttinger. Density of electornic levels in disordered systems //Phys. Rev. B., 1975, v.12, №10, p.4460-4474) :
| (8.3) |  |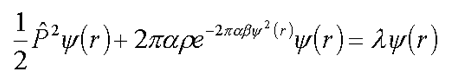
В случае a<о (притягивающий потенциал) уравнение (8.3) имеет нетривиальные решения. На рис.1 показана зависимость l от fo ( /2/ , см. также уравнения (7.1) в разделе “Нелинейные уравнения самосогласованных состояний“):
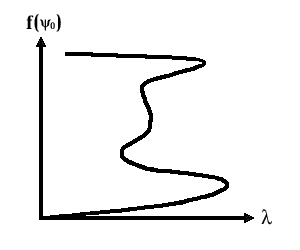
Рис.1. Многозначность решения нелинейной краевой задачи
( где: f(y0)=[ln(1+y20)]1/2, y0=y(0) )
Из вида кривой на рис.1 следует, что существует область значений параметров, при которых одновременно сосуществуют шесть различных основных состояний (решений уравнения (8.3) без узлов). Эти результаты свидетельствуют о необычных свойствах нелинейных уравнений квантовой механики.