Нелинейные уравнения самосогласованных состояний
Вычислительные методы решения нелинейной краевой задачи в теории полярона
Математическим объектом в секторе квантово-механических систем являются исследования на классе многопараметрических нелинейных краевых задач на собственные значения для системы интегродифференциальных уравнений, моделирующих критические режимы в физических и биологических процессах.
Объектами исследования являются:
– спектральная задача для системы интегродифференциальных уравнений
| (А) |  |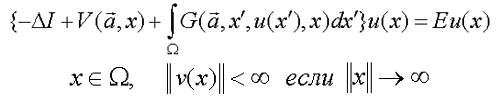
– объединенные системы для нелинейной краевой задачи (Б) и спектральной задачи (В)
| (Б) |  |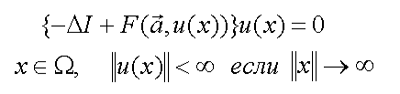
| (В) |  |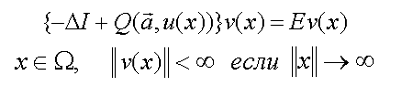
где :
W – это область значений х с бесконечной границей;
a – вектор физических параметров модели;
E – спектральный параметр (E=E(a));
I – единичный вектор.
Вышеперечисленные задачи представляют собой новый класс математических объектов с некоторыми общими характеристиками (нелинейность, сингулярность, многопараметричность на внешних физических параметрах, многомерность конфигурационного пространства и существование более одного решения). В целом указанные задачи можно охарактеризовать как класс нелинейных задач, описывающих эволюцию сложных систем с бифуркациями и критическими режимами.
В данном разделе представлены некоторые примеры задач (А), (Б) и (В).
1. Уравнение f3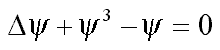
1.1. Сферически-симметричные решения в R3 ( /4/ )
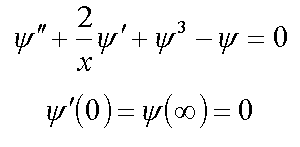
1.2. Сферически-симметричные решения в R2 ( 2* )
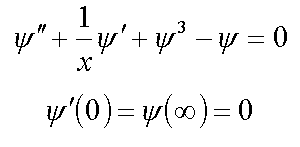
1.3. Сферически-несимметричные решения ( 3* )
2. Полярон сильной связи
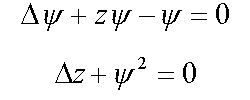
2.1. Сферически-симметричные решения в R3 ( /1/ , /2/ )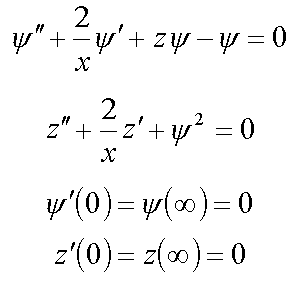 
2.2. Сферически-несимметричные решения ( /11/ , /12/ )
3. Уравнение для связанного конденсона ( 4* )
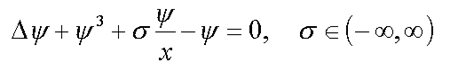
3.1. сферически-симметричные решения в R3 ( 4* )
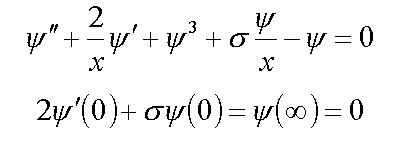
3.2. Сферически-несимметричные решения
4. Уравнение для F-центра
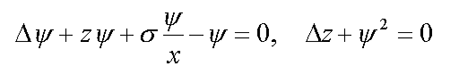
4.1. Сферически-симметричные решения в R3 ( /3/ , /5/ )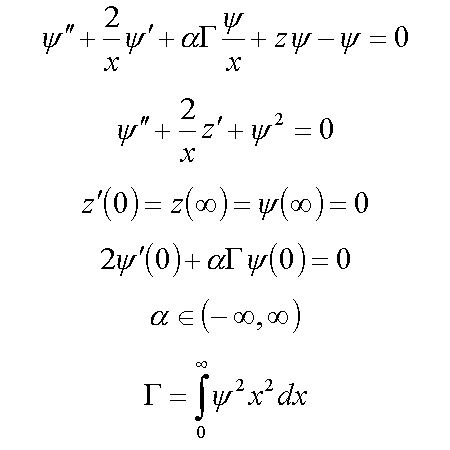 
4.2. Сферически-несимметричные решения ( /11/ , /12/ )
5. Поляронный конденсон ( 4* )
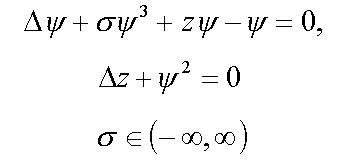
6. Связанный поляронный конденсон ( 4* )
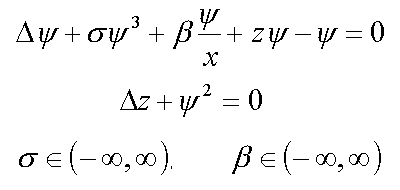
7. Электрон в неупорядоченной среде с потенциалом притяжения ( 1* )
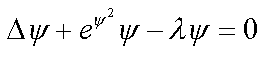
7.1. Сферически-симметричные решения в R3
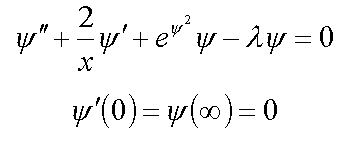
8. Электрон в неупорядоченной среде с потенциалом отталкивания ( 1* )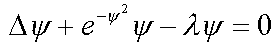 
1. Сферически-симметричные решения в R3 ( 6* )
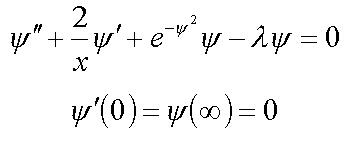
9. Континуальный экситон
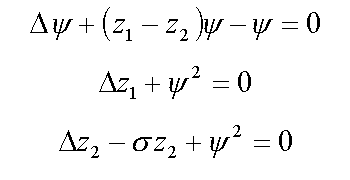
9.1. Сферически-симметричные решения в R3 ( /8/ , /10/ )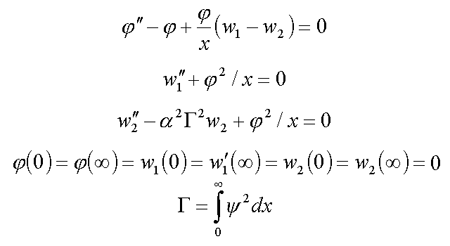 
9.2. Сферически-несимметричные решения в R3 ( 7* )
10.Континуальный биэкситон
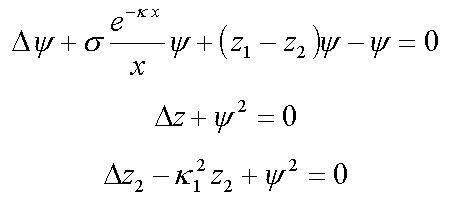
10.1. сферически-симметричные решения ( /14/ , 7* )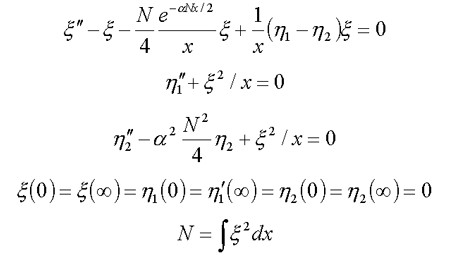 
10.2. Сферически-несимметричные решения
11. Сольватированный электрон
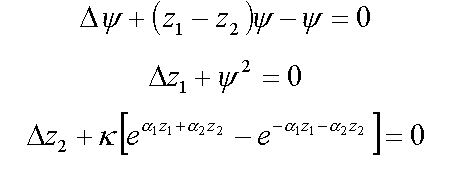
11.1. Сферически-симметричный случай ( /8/ )
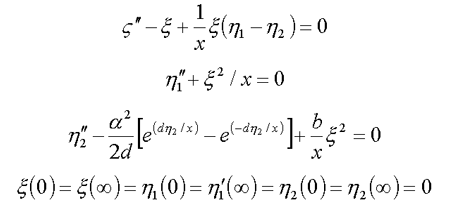
12. Нуклон в мезонном поле
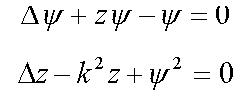
12.1. Сферически-симметричные решения в R3 ( /9/ , /13/ )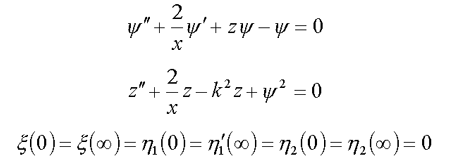
12.2. Сферически-несимметричные решения в R2 ( 5* )
12.3. Сферически-симметричные решения для нуклона в ядре ( /15/ )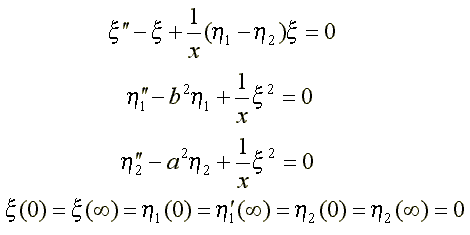
13. Биполяронный экситон
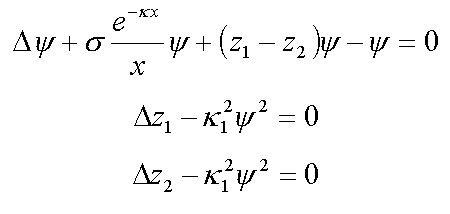
14. Нелинейные уравнения протяженных электронных состояний в белке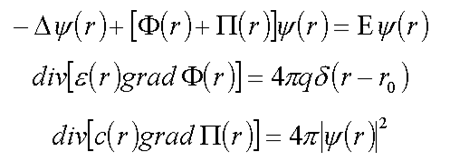 
Функции e(r), c(r) являются заданными ( /6/ ).
15. Уравнения для частиц в квантовом поле при произвольной силе связи ( /7/ )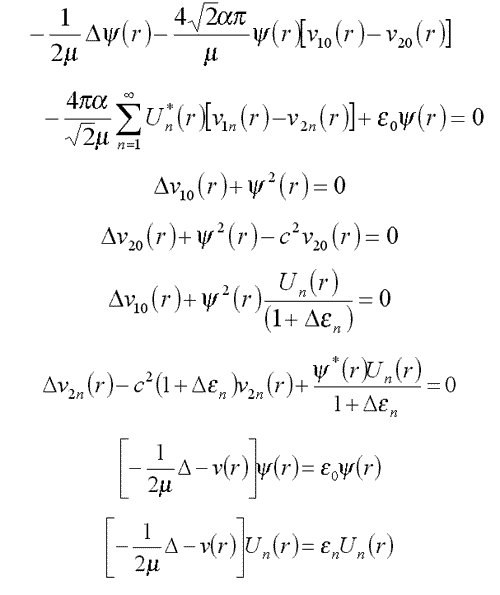 
16. Уравнения для флуктуонов
16.1. Общий случай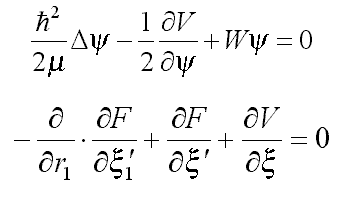 
16.2. В условиях применимости термодинамического разложения Ландау-Гинзбурга-Девоншира (ЛГД) (9.1) в сферически-симметричном случае (16.1) имеет вид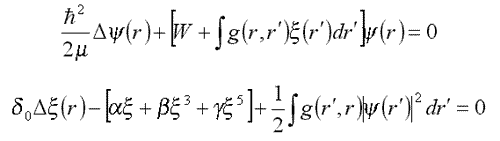 
где
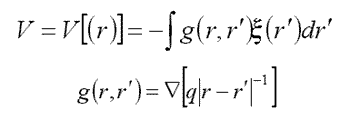
Флуктуон при малых гомофазных флуктуациях: g(r,r’ )= g0(r-r’).
F[x]=ax2 приводит к уравнению для дейтрона (12.1).
16.3. Флуктуон Кривоглаза
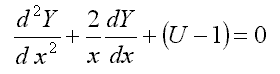
где
.
17.1. Электрон в ДНК ( /16/, /18/ )
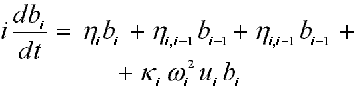
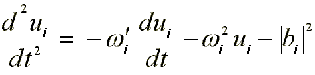
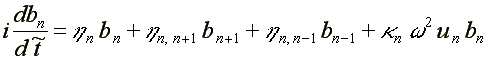
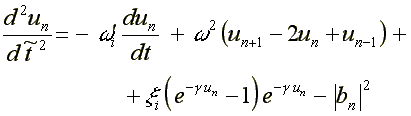
где: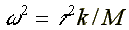
17.2. Электрон в фотореакционном центре фотосинтеза ( /17/, /19/ )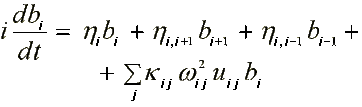 
–
————–
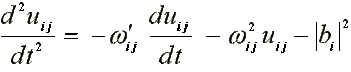1* – R.Friedberg, J.M.Luttinger. Density of electornic levels in disordered systems //Phys. Rev. B., 1975, v.12, №10, p.4460-4474
2* – Дж.Уизем. Нелинейные волны. – Москва: Мир, 1977
3* – Г.Л.Алфимов, В.М.Елеонский, Н.Е.Кулагин, Л.М.Лерман, В.П.Силин. Двумерные самолокализованные решения уравнения Du-u+u3=0 : препринт №238. – Москва: Физический институт АН СССР, 1988, с.27;
4* – А.С.Давыдов. Теория твёрдого тела. – Москва: Наука, 1976
5* – К.А.Горшков, В.А.Миронов, А.М.Сергеев. Нелинейные волны, самоорганизация. – Москва: Наука, 1983, с.112-128
6* – И.М.Лившиц, С.А.Гредескул, Л.А.Пастур. Введение в теорию неупорядоченных систем. – Москва: Наука, 1982
7* – I.V.Amirkhanov, I.V.Puzynin, T.P.Puzynina, E.V.Zemljanaja. Iteration method for solving the spherical non-symmetrical polaron equation // Polarons & Applications / Ed. V.D.Lakhno. – Wiley, 1993
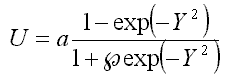