Биполяроны
Сольватированные электроны в электролитах
Электронные состояния в неупорядоченных системах
Биполярон представляет собой два связанных полярона, он может образовываться в ионных кристаллах, жидкостях, полупроводниках и неупорядоченных системах. Для случая ионных кристаллов точное решение проблемы биполярона было найдено в работах /4/ и /11/ , когда взаимодействие двух электронов с фононным полем описывается гамильтонианом Пекара-Фрёйлиха:
| (10.1) | 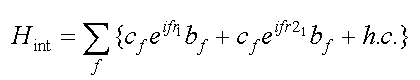 |
где r1 и r2 — координаты первого и второго электронов, соответственно.
Полуфеноменологическая биполяронная теория предполагает, что в адиабатическом пределе оба электрона движутся в одной и той же потенциальной поляронной яме, образованной их быстрыми колебаниями в ней. Поэтому взаимодействие между электроном и поляризацией имеет вид:
| (10.2) | F(r1, r2) = F(r1) + F(r2) |
Это уравнение не обладает трансляционной инвариантностью и соответствует феноменологическому подходу, при котором потенциальная поляронная яма предполагается фиксированной в некоторой области пространства. В работах /4/ и /11/ была разработана последовательная адиабатическая трансляционно-инвариантная биполяронная теория, основанная на адиабатической теории Боголюбова-Тябликова. Согласно этому подходу в адиабатическом пределе движения электронов в биполяроне разделяются. Относительные координаты электронов описывают быстрые колебания этих электронов в потенциальной яме, которая имеет форму их эффективного взаимодействия:
| (10.3) | F(r1, r2) = F(r1 — r2) |
Координаты центров масс электронов описывают медленные движения электронов. В этом случае поляронная яма не фиксирована в пространстве, а следует адиабатически за движением электронного центра масс. Взаимодействие (10.3) автоматически является трансляционно-инвариантным. На рис.1 показаны частицеподобные решения нелинейных уравнений биполярона (см. уравнение (4.1) в разделе «Нелинейные уравнения самосогласованных состояний«). Эти решения дают величину критического параметра ионной связи h=0.31 (h=e╔/e0, где e╔, e0 — высокочастотная и статическая диэлектрическая проницаемость ионного кристалла). Результаты, полученные для трехмерного полярона, также справедливы и для биполярона в двумерном пространстве. Также были найдены энергия двумерного биполярона и критические величины констант электронно-фононных связи, при которых биполяронные состояния стабильны.
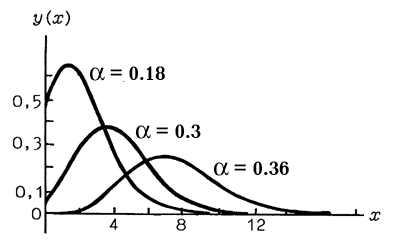
Рис.1. Частицеподобные решения для биполяронного уравнения
для биполярона при различных значениях параметра a
В статье /1/ и монографии «Excited polaron states in condensed media« были рассмотрены возможные состояния биполярона в суперионных полупроводниках. В биполяронной модели сверхпроводимости получена оценка сверхпроводящей температуры перехода Тc. В частности, для высокотемпературного сверхпроводника YBa2Cu3O6+x была найдена корректная зависимость Тc от стехиометрии по кислороду x. Возможности образования биполяронных состояний в полупроводниках с примесями были проанализированы в статье /6/ и монографии «Polarons & Applications«.