Исследования по нерелятивистской квантовой теории поля
Автолокализованные состояния в магнитоупорядоченных системах
Вычислительные методы решения нелинейной краевой задачи в теории полярона
Основы нерелятивистской квантовой теории поля в случае сильного взаимодействия частицы и поля были заложены в работах Боголюбова и Тябликова. Особую значимость эти работы приобрели в настоящее время в связи с проблемой квантования полей в окрестности ненулевых классических решений и непертурбативными решениями квантовой теории поля.
Теоретические работы по нерелятивистской квантовой теории поля в СКМС связаны с исследованием гамильтониана (1.1) :
| (1.1) | 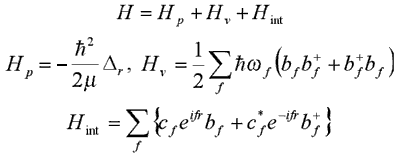 |
где
Hp, Hn и Hint — гамильтонианы свободной частицы, поля и взаимодействия между частицей и полем соответственно;
m — масса частицы;
r — координаты частицы;
b+, b — операторы рождения и уничтожения квантов поля с энергией hwf ;
cf — некоторые постоянные, характеризующие взаимодействие частицы с полем.
Несмотря на то, что гамильтониан (1.1) является наиболее простым для нерелятивистской частицы, точное решение проблемы (1.1) в настоящее время отсутствует.
Гамильтониан (1.1) лежит в основе теории полярона (медленный электрон в ионном кристале): описывает взаимодействие электронов проводимости с поляризацией в пьезоэлектрических полупроводниках (пьезополяроны); взаимодействие электронов с акустическими колебаниями в гомеополярных кристаллах (конденсоны). В молекулярных кристаллах гамильтониан (1.1) описывает взаимодействие с оптическими колебаниями. В ядерной физике гамильтониан (1.1) описывает взаимодействие нуклонов с мезонным полем. Ссылки на эти и другие области применения гамильтониана (1.1) содержатся в сборнике трудов «Возбужденные поляронные состояния в конденсированных средах» и монографии «Excited polaron states in condensed media».
Работы СКМС по нерелятивистской теории поля были сосредоточены на решении нелинейных интегродифференциальных уравнений Боголюбова-Тябликова, которые вытекают из (1.1) в пределе сильного взаимодействия частицы и поля :
| (1.2) | 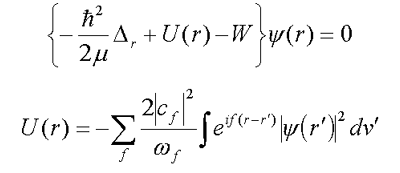 |
В работах /1/ и /2/ были впервые найдены сферически симметричные частицеподобные решения (1.2) в случае полярона. Несферические решения (1.2) были найдены в /33/ и /35/ (Рис.1а). На Рис.1б схематически представлены решения типа 2s, 3d и 2s│3d, обладающие топологией, отличной от водородоподобной серии. В работах /28/ и /34/ исследовались ветвления решений нелинейного уравнения (1.2) и их связь с устойчивостью возбужденных состояний частицы в поле.
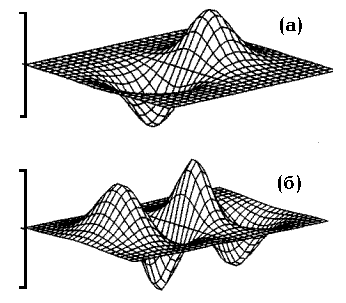
Рис.1а. Несферические волновые функции полярона,
аналогичные «2p» (a) и «3p» (b) типам
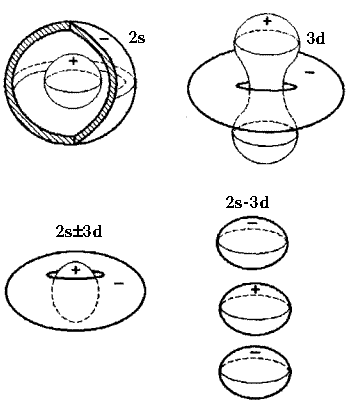
Рис.1б. Схематическое представление самосогласованных
поляронных состояний смешанной симметрии 2s│3d