Вычислительные методы решения нелинейной краевой задачи в теории полярона
Исследования по нерелятивистской квантовой теории поля
Нелинейные уравнения самосогласованных состояний
В пределе сильной связи вычисление характеристик полярона (энергетических уровней и волновых функций) можно свести к нелинейной системе дифференциальных уравнений на собственные значения. К настоящему времени хорошо изучены сферически-симметричные решения некоторых типов нелинейных дифференциальных уравнений, возникающих в теории полярона (см. раздел «Нелинейнейные уравнения самосогласованных состояний«). В работах /1/ , /2/ , /3/ , /4/ , /5/ , /6/ для простейшего случая системы двух уравнений был использован пристрелочный алгоритм по отношению к двум параметрам f’ и z’ при x=0, которые определяют задачи Коши. Эти параметры были уточнены таким образом, чтобы соответствующие численные решения задачи Коши могли удовлетворять граничным условиям при x╝╔.
Исследование несимметрических конфигураций в случае проблемы полярона (см. раздел «Исследования по нерелятивистской квантовой теории поля«) или в случае протяженных электронных состояний в биомакромолекулах, когда атом металла и глобула имеют различные центры симметрии, приводит к многомерной вычислительной задаче. Она была решена с помощью следующего алгоритма ( /9/ ). Дифференциальные уравнения в частных производных были аппроксимированы конечноразностными уравнениями. Полученная нелинейная задача была решена продолжением по параметру. В этом случае мы столкнулись с необходимостью решать линейные задачи с плохо определенными матрицами чередующегося знака. Используя быстрое обращение оператора Лапласа, мы смогли заменить каждую такую задачу на эквивалентную ей «хорошую» задачу (с хорошо определенной матрицей фиксированного знака), которая затем решалась методом итерации. Эта процедура позволяет довольно быстро решать нелинейные задачи (в ряде задач — приблизительно за число операций, пропорциональное числу точек в решении) — это делает алгоритм применимым для двух- и трехмерных задач.
При численном исследовании задачи можно исходить из того, что решения являются гладкими. Поэтому их разложения по сферическим гармоникам должны быстро сходиться и можно ожидать хорошего приближения несколькими первыми членами ряда. Соответствующие проекционные (Галеркинские) уравнения представляют собой интегродифференциальные уравнения, которые можно заменить дифференциальными. Основная трудность при решении этих уравнений состоит в том, что они имеют неединственное решение и интерес представляют несколько таких решений.
Нелинейные уравнения типа поляронного обладают замечательной особенностью: простые преобразования подобия позволяют получить эквивалентную задачу, не содержащую собственного значения. При нахождении решений в последнюю задачу можно искусственно ввести параметр (s). Точнее, в правой части уравнений (вместо нуля) записывается f(r)*s , где f(r) — некая предписанная функция. В данной задаче реализуется процедура продолжения по параметру s. В качестве отправного решения можно брать тривиальное решение и положить s=0. В процессе продолжения параметр s меняется немонотонно: при прохождении «точек поворота», отвечающих бифуркациям слияния двух решений, направление движения по s меняется на противоположное. Каждый раз, когда в процессе продолжения s обращается в 0, получается решение нужной нам задачи.
Безусловно, численное решение краевой задачи осуществляется на конечной области пространства R3. В отличие от промежуточных (при ненулевых s) нужные решения (при s=0) не меняются при асимптотическом увеличении области интегрирования ( /7/ , /8/ ).
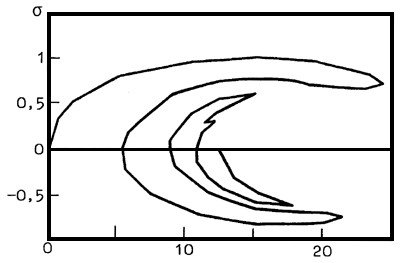
Рис.1. Типичная зависимость квадрата нормы решения от параметра s
На рис.1 показаны несферические решения системы уравнений (см. пункт 2 раздела «Нелинейнейные уравнения самосогласованных состояний») для полярона, которые были найдены с помощью вышеописанного алгоритма.
Обычно вычислительные задачи, связанные с изучением свойств поляронных уравнений, требуют использования всех ресурсов суперкомпьютеров. Это особенно относится к фундаментальным проблемам поляронной теории, таким как трехмерная нелинейная краевая задача (см. раздел «Нелинейнейные уравнения самосогласованных состояний») и распределение фононных частот для сферически-несимметричных распределений электронной плотности. Вычисление ренормализованных мезонных полей в теории дейтронного квантового поля (см. раздел «Исследования по нерелятивистской квантовой теории поля») позволило бы ответить на фундаментальный вопрос о возможности теории сильного взаимодействия без расходимостей.