Dynamics of a crystal lattice with defects
Review of the studies carried out
Solutions to (1.2) (see “Investigations on the nonrelativistic quantum field theory”) with v(r) replaced by U, such that
| (3.1) | 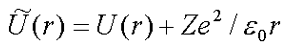 |
where e0 is the crystal’s dielectric permittivity, may be of importance in explaining the nature of relaxed excited states of colour centers and provide interpretation to numerous experiments on photoexcitation, luminescence and photoconductivity of ionic crystals with F-centers.
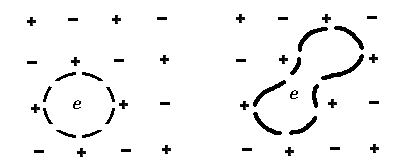
Spherically-symmetric solutions, corresponding to excited self-consistent states and their role in photoexcitation are studied in /1/ , /2/ , /3/ for the simplest case of the F-center (Fig.1b). More complex centers, such as the F+2-center (Fig.1b) require finding of non-spherical solutions to nonlinear integrodifferential equations.
One of the central problems of the crystal lattice’s dynamics is calculation of its oscillation spectrum for the case, when the lattice contains various defects and impurities. In terms of the lattice’s dynamics the presence of an excess electron (polaron) in the crystal interacting with the lattice’s oscillations, can be considered as a special-type defect.
In /6/ , /8/ , /9/ we found solutions to the integrodifferential equation
| (3.2) | 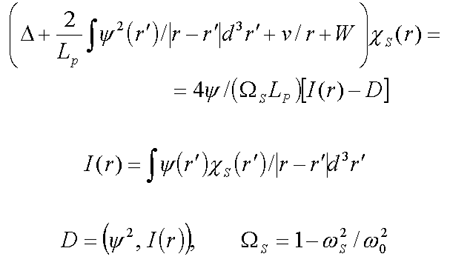 |
describing frequencies ws of the lattice’s local phonons in the presence of a bound polaron state (F-center). Fig.2a and Fig.2b show the distribution of the bound phonon frequency spectrum for the ground and the first self-consistent states of the F-center in KCl, calculated from (3.2).
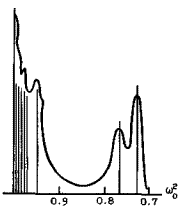
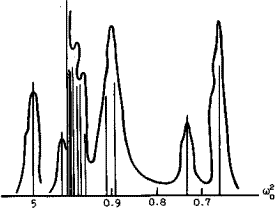
Fig.2b. . Density distribution of the bound phonon frequency spectrum for the first self-consistent state of the F-center in KCl
The frequency spectra obtained provide the basis for calculation of a large body of optical effects: Raman spectrum intensity, light absorbtion by F-centers, luminescence and other phenomena ( /11/ ).