Nonlinear equations of nonrelativistic quantum mechanics

Publications on the subject

The mathematical object of investigation in LQS is the study on a class of multiparameter nonlinear boundary value problems for the system of integrodifferential equations modeling critical regimes in physical and biological proceses.
The objects of research are:
– The spectral problem for the system of integro-differential equations

 

(A)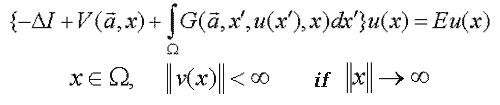

– The joint systems for the nonlinear boundary value problem (B) and the spectral problem (C)

 

(B)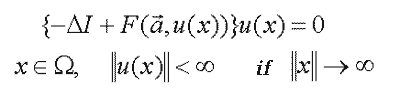

(C)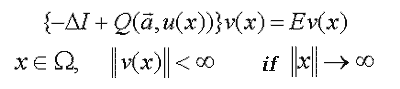

where :
W – is a domain of х with indefinite boundary;
a – is the vector of the model’s physical parameters;
E – is the spectral parameter (E=E(a));
I – is the unit operator.

The above mentioned problems represent a new class of mathematical objects with some common characteristics such as non-linearity, singularity, multiparametricity on external physical parameters, multidimensionality of configuration space and nonuniquehess of solutions. On the whole, the enumerated problems can be characterized as a class of nonlinear problems, wich describes the evolution of complicated systems with bifurcations and critical regimes.
Some examples of (A), (B) and (C) are represented in this section.

1. Equation f³

 

   1.1. Spherically-symmetric solutions in R³ ( /4/ )

   1.2. Spherically-symmetric solutions in R² ( 2* )

   1.3. Spherically-unsymmetric solutions ( 3* )

---

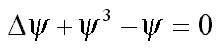
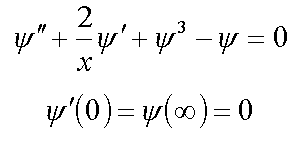
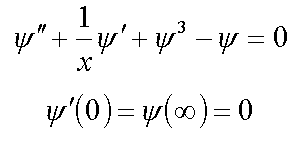
2. Strong-coupling polaron

   2.1. Spherically-symmetric solutions in R³ ( /1/ , /2/ )

   2.2. . Spherically-unsymmetric solutions ( /11/ , /12/ )

---

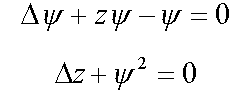
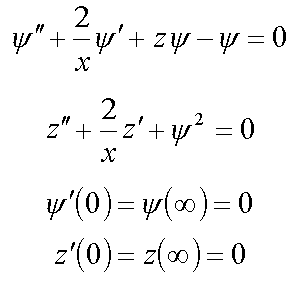
3. Equation for bound condenson ( 4* )

   3.1. Spherically-symmetric solutions in R³ ( 4* )

   3.2. Spherically-unsymmetric solutions

---

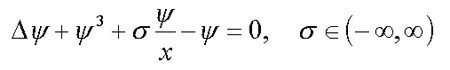
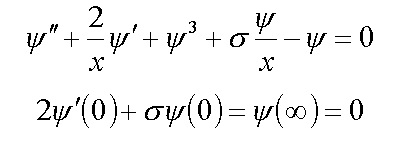
4. Equation for F-center

   4.1. Spherically-symmetric solutions in R³ ( /3/ , /5/ )

   4.2. Spherically-unsymmetric solutions ( /11/ , /12/ )

---

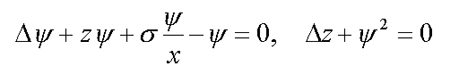
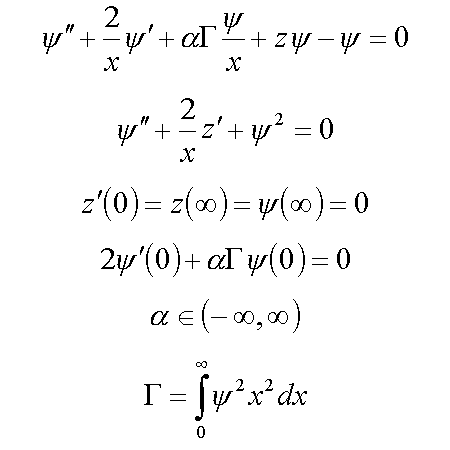
5. Polaronic condenson ( 4* )

---

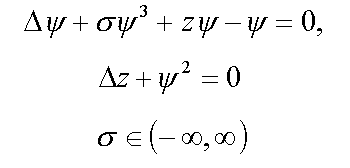
6. Bound polaronic condenson ( 4* )

---

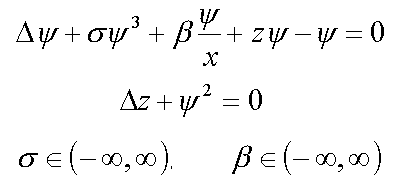
7. Electron in disordered medium with ( 1* )

   7.1. Spherically-symmetric solutions in R³

---

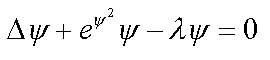
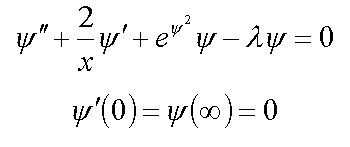
8. Electron in disordered medium with repulsoin potential ( 1* )

   1. Spherically-symmetric solutions in R³ ( 6* )

---

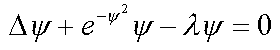
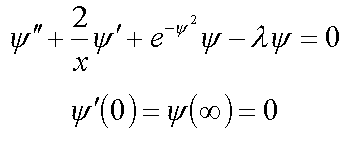
9. Continuum exciton

   9.1. Spherically-symmetric solutions in R³ ( /8/ , /10/ )

   9.2. Spherically-unsymmetric solutions in R³ ( 7* )

---

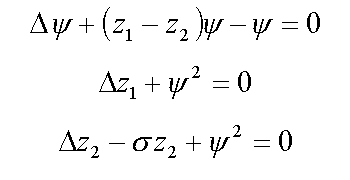
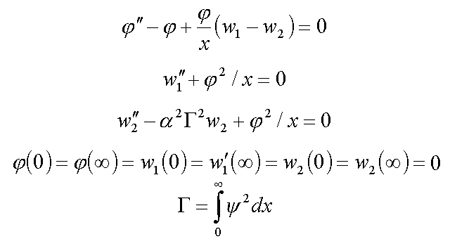
10. Continuum biexciton

   10.1. Spherically-symmetric solutions ( /14/ , 7* )

   10.2. Spherically-unsymmetric solutions

---

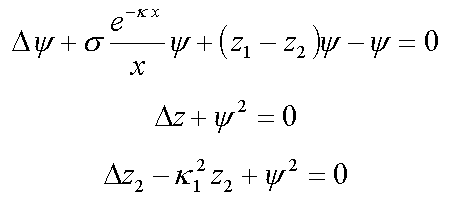
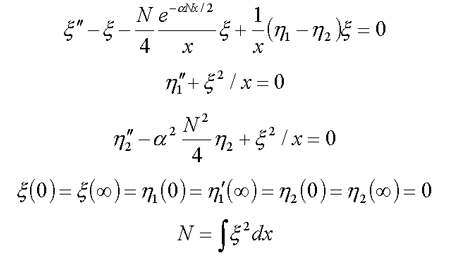
11. Solvated electron

   11.1. Spherically-symmetric case ( /8/ )

---

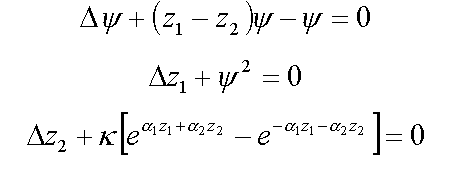
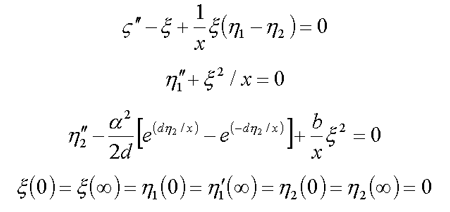
12. Nucleon in scalar meson field

   12.1. Spherically-symmetric solutions in R³ ( /9/ , /13/ )

   12.2. Spherically-unsymmetric solutions in R² ( 5* )
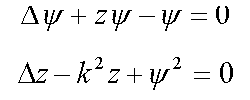
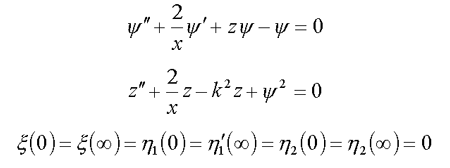
12.3. Spherically-symmetric solutions for nucleon in the nucleus ( /15/ )

---

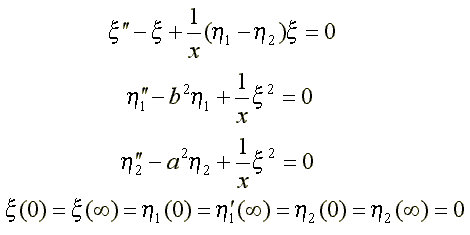
13. Bipolaronic exciton

---

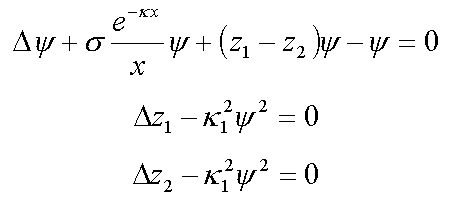
14. Nonlinear equations of electron extended ststes in proteins

     Functions e(r), c(r) are predetermined ( /6/ ).

---

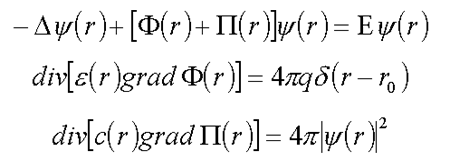
15. Equationa for particles in a quantum field at arbitrary strength of coupling ( /7/ )

---

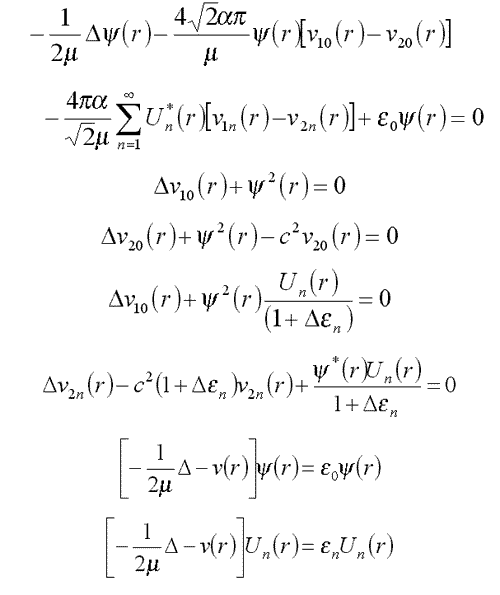
16. Equations for fluctuons
16.1. General case

   16.2. In the context applicability of Landau-Ginzburg-Devonshire (LGD) thermodynamic expansion (9.1) in the spherically-symmetric case (16.1) has the form

where

Fluctuon for small homophase fluctuations: g(r,r’)=g₀(r-r’).
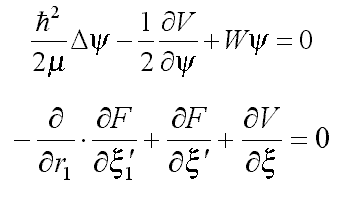
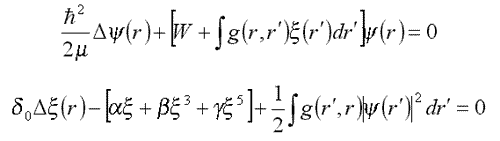
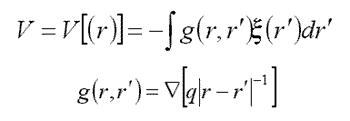
F[x]=ax² leads to the equation for deuteron (12.1).
16.3. Krivoglaz fluctuon

where

.
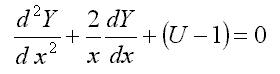
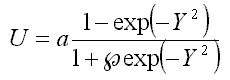
17. Discrete models
17.1. Electron in DNA ( /16/, /18/ )

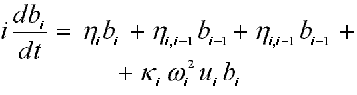
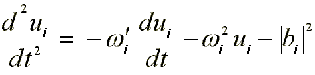
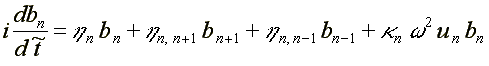
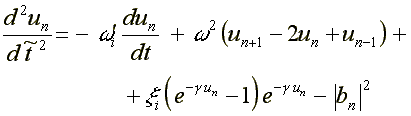
where:
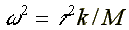   17.2. Electron in the photoreaction center of the photosyntesis ( /17/, /19/ )

---

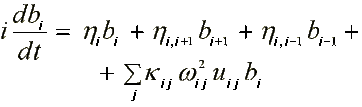
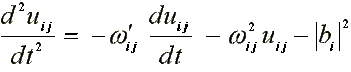
1* – R.Friedberg, J.M.Luttinger. Density of electornic levels in disordered systems //Phys. Rev. B., 1975, v.12, №10, p.4460-4474
2* – J.Wisem. Nonlinear waves. – Moscow : Mir, 1977 ( in Russian )
3* – G.L.Alfimov, V.M.Eleonsky, N.E.Kulagin, L.M.Lerman, V.P.Silin. Two-dimensional self-localized solutions of the equation Du-u+u³=0 : Preprint №238. – Moscow : Physical Institute of the USSR Academy of Sciences, 1988, p.27 ( in Russian )
4* – A.S.Davydov. Solid state theory. – Moscow : Nauka, 1976 ( in Russian )
5* – K.A.Gorshkov, V.A.Mironov, A.M.Sergeev. Nonlinear waves, self-organization. – Moscow : Nauka, 1983, с.112-128 ( in Russian )
6* – I.M.Livshits, S.A.Gredeskul, L.A.Pastur. Introduction into the theory of disordered systems. – Moscow : Nauka, 1982 ( in Russian )
7* – I.V.Amirkhanov, I.V.Puzynin, T.P.Puzynina, E.V.Zemljanaja. Iteration Method for Solving the Spherical Non-symmetrical Polaron Equation (The Luttinger LU Model) // Polarons & Applications / Ed. V.D.Lakhno. – Leeds: J.Wiley & Sons Ltd, 1994, p.445-453

Publications on the subject