Numerical methods for solution of nonlinear boundary problems in the polaron theory
In the strong coupling limit calculation of polaron characteristics (energy levels and wave functions) can be reduced to a nonlinear system of eigen-value differential equations. Spherically-symmetric solutions of some types of nonlinear differential equations, arising in the polaron theory have been much studied by now (see also “Nonlinear equations of nonrelativistic quantum mechanics”). In the simplest case of two-equation system we used in /1/ , /2/ , /3/ , /4/ , /5/ , /6/ a shooting algorithm with respect to the two parameters f’, z’ at x=0, determining the Koshi problem. These parameters were refined so that the corresponding numerical solutions of the Koshi problem might satisfy the boundary conditions as x╝╔.
The study of unsymmetrical configurations in the case of polaron problem (see also “Investigations on the nonrelativistic quantum field theory”) or in the case of extended electron states in biomacromolecules, when the metal’s atom and the globule have different centres of symmetry, leads to a multidimensional calculation problem. It had been solved by the following algorithm ( /9/ ). Differential equations in partial derivatives were approximated by finite difference equations. The nonlinear problem obtained was solved by parameter continuation. In this case we came up the necessity to solve linear problems with not rather attributed matrices of alternating signe. Using fast reverse of Laplase operator we could replace each such problem by an equivalent “good” one (with well attributed matrix of fixed signe), which was solved by the iteration method. This procedure allowed rather a quick solution of linear problems (in a number of operations approximately proportional to the number of points in the grid) which made the algorithm useful for two-and three-dimensional problems.
In numerical analysis of the problem one can proceed from the fact, that solutions are smooth (analytical). Therefore their expansions in terms of spherical harmonics have a quick convergence and one might expect a good approximation by some first terms of the series. The corresponding projection (Galerking) equations are integrodifferential equations which can be replaced by differential ones. The main difficulty in their solution is in the fact that they have more than one solutions and some of these solutions may be of interest.
Nonlinear polaron-type equations have a remarkable feature: simple similarity transformations allow to get an equivalent problem, but without the eigen value. When searching for a solution we can introduce a parameter (s) into the latter problem. More precisely, in the right-hand side of our equations we can write down f(r)*s (instead of 0), where f(r) is a certain prescribed function. In this problem the procedure of parameter s continuation is realized. As a starting solution we can take a trivial one and s=0. In the course of continuation the parameter s changes nonmonotonously: in passing through the “reverse point” corresponding to bifurcations of confluence of 2 solutions, the direction of motion along s is reversed. Each time, when s turns to zero, we have a solution to our problem (Fig.13). Of course, the numerical solution of the boundary problem is performed for a finite region of space R3. As distinct from intermediate solutions (at s№0), the solutions we are searching for (at s=0) do not change as the integration region asymptotically increases ( /7/ , /8/ ).
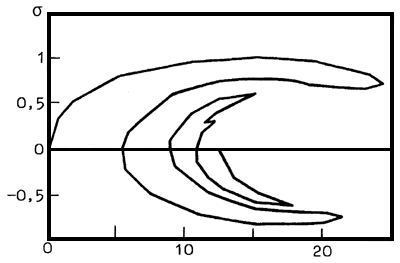
Fig.1. Typical dependence of the squared of norm of solution on parameter s
Generally, calculation problems concerned with the study of polaron equation properties require complete resources of supercomputers. This is especially true for fundamental problems of the polaron theory, i.e. the three-dimensional nonlinear boundary problem (see also “Investigations on the nonrelativistic quantum field theory”) and the phonon frequencies distribution for spherically asymmetric electron density distributions. Calculation of renormalized meson fields in the deuteron quantum field theory (Sect.II) would allow to solve the fundamental problem of the possibility of the strong-interaction theory without divergencies.