Investigations on the nonrelativistic quantum field theory
Review of the studies carried out
The foundations of the nonrelativistic quantum field theory for strong particle-field interaction were laid by Bogolubov-Tyablikov. Nowadays their works are taking on great significance in the context of the field quantization problem in the vicinity of nonzero classical solutions and with regard to nonperturbative solutions of the quantum field theory.
Theoretical works of the LQS in this field are connected with the study of Hamiltonian (1.1) :
| (1.1) | 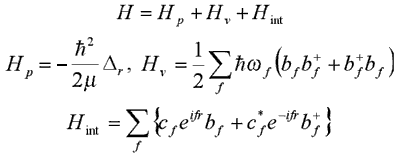 |
where
Hp, H n and Hint– are the Hamiltonians of a free particle, the field, and the particle-field interaction, respectively;
m – is the particle’s mass;
r – is its coordinates;
b+, b – are operators of creation and annihilation of the field quanta with the energy hwf ;
cf – are some constants of the particle-field interaction.
Despite the fact that Hamiltonian (1.1) is the simplest for the non-relativistic particle, its exact solution is not yet at hand.
Hamiltonian (1.1) is basic for the polaron theory (slow polaron in an ionic crystal); it describes interaction of conductivity electrons with polarization in piezoelectric semiconductors (piezopolarons) and interaction of electrons with acoustic oscillations in homeopolar crystals (condensons). In molecular crystals it determines interaction with optical oscillations and in nuclear physics – interaction of nucleons with the meson field. Details of Hamiltonian (1.1) application may be found in “Excited polaron states in condensed media” and “Excited polaron states in condensed media”.
Much of LQS current interest was centred on the solution of nonlinear integrodifferential Bogolubov-Tyablikov equations :
| (1.2) | 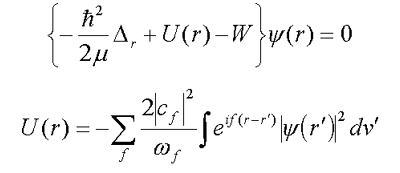 |
which follow from (1.1) in the limit of strong particle-field interaction.
In /1/ and /2/ spherically-symmetric particle-like solutions to (1.2) were first found for the polaron. Non-spherical solutions to (1.2) were obtained in /33/ and /35/ (Fig.1a). Fig.1b shows schematically solutions of the 2s, 3d and 2s╠3d, types, whose topology is different from the hydrogen-like series. In /28/ and /34/ we studied branchings of solutions to nonlinear equation (1.2) and established their relation to the stability of particle’s excited states in the field.
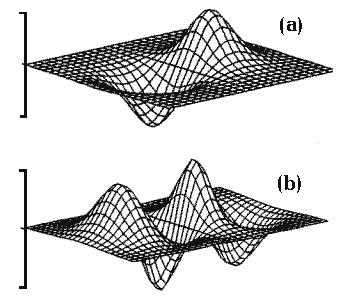
“2p” (a) and “3p” (b) polaron types
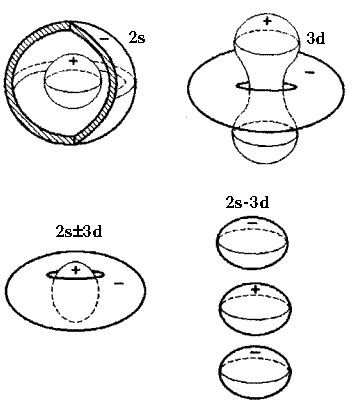
polaron states with mixed symmetry 2s╠3d