Ferroactive models of ion channels in biomembranes

Publications on the subject

One of the actual problems of contemporary mathematical biophysics is to study the structures of biological membranes and to understand their functioning. Among various functions of biomembranes the transport one may be considered as the most important. The ferroactive model, developed in SQMS allows a qualitative interpretation to a wide range of experimental data on the functioning of ion channels in biomembranes. In the modern view the role of channels in biomembranes is played by embedded proteins. Thus, four homologous domains were identified in the protein structure of Na⁺-channels from the electric organ of the eel electrophorus electricus. Each of them contained five hydrophobous and amphiphilous segments and one segment with a characteristic strong positive charge (Fig.10).

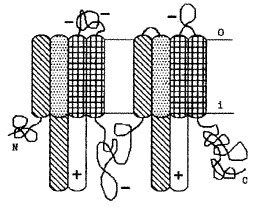
Fig.10. Domain organization of the Nа⁺-channel primary structure.   In this case it is thought that the ion pore is formed by twisting of homologous domains into a cylinder structure. The availability of polarization, comparable in size with well khown values for the ferroelectric liquid crystals and significant non-linearity of the biomembrane’s media near the phase transitions necessitate us to consider ferroactive models of the biomembrane’s ion channel. The simplest ferroactive model of the channel, developed in /1/, /3/ and /4/ is based on the Landau-Ginzburg-Khalatnikov equation:

 

(9.1)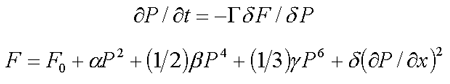

where a, b, g are coefficients of the Landau-Ginzburg- Devonshire thermodynamical expansion. The solutions of (9.1) are of the Kink-form :

 

(9.2)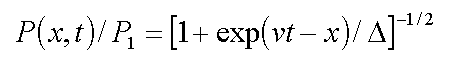

In the stationary case this corresponds to the appearance of a boundary between phases, when the temperature goes upward from the stable state with the minimum F at P=P₁ (ferrophase) to the stable state with the maximum P=P₂=0 (paraphase), or when the paraphase region arises in the ferrophase. It is essential, that the kink motion of the interphase boundary is possible only in a short temperature interval [T^*;Т_c] with respect to the Kurie-Veiss temperature T_c :

 

(9.3)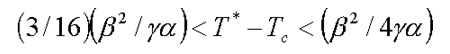

Within our model the channel’s functioning may be presented as follows. The availability or occurrence of a charged ion near the emerged interphase boundary may lead to its binding with the boundary, followed by its carrying inside the membrane, which moves along the ion channel. The analogous picture, but with reverse movement of the interphase boundary appears on a certain cooling of the system. Ferrophase arises on the inside of the membrane and starts gradual propagating along the ion channel to the outside of the membrane.
The model developed is explanatory for gate currents, singular behaviour of dielectric permittivity near the Tc , the existence of boundaries between different phases, etc.

Publications on the subject