Nonlinear equations of nonrelativistic quantum mechanics
The mathematical object of investigation in LQS is the study on a class of multiparameter nonlinear boundary value problems for the system of integrodifferential equations modeling critical regimes in physical and biological proceses.
The objects of research are:
– The spectral problem for the system of integro-differential equations
| (A) | 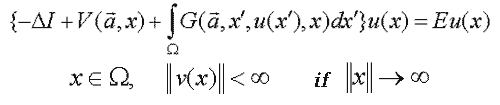 |
– The joint systems for the nonlinear boundary value problem (B) and the spectral problem (C)
| (B) | 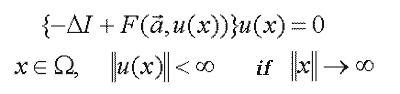 |
| (C) | 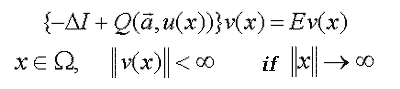 |
where :
W – is a domain of х with indefinite boundary;
a – is the vector of the model’s physical parameters;
E – is the spectral parameter (E=E(a));
I – is the unit operator.
The above mentioned problems represent a new class of mathematical objects with some common characteristics such as non-linearity, singularity, multiparametricity on external physical parameters, multidimensionality of configuration space and nonuniquehess of solutions. On the whole, the enumerated problems can be characterized as a class of nonlinear problems, wich describes the evolution of complicated systems with bifurcations and critical regimes.
Some examples of (A), (B) and (C) are represented in this section.
1. Equation f3
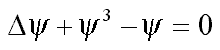
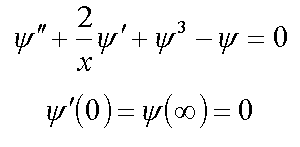
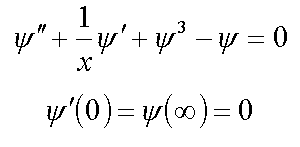
2. Strong-coupling polaron
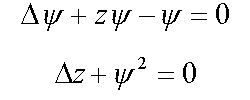
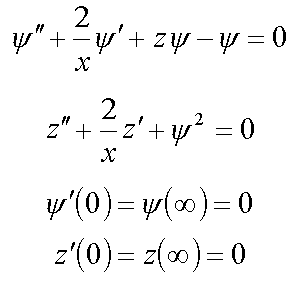
3. Equation for bound condenson ( 4* )
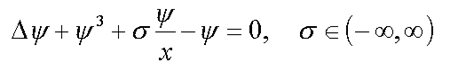
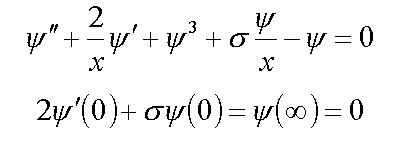
4. Equation for F-center
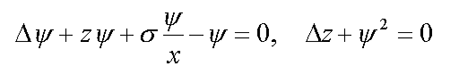
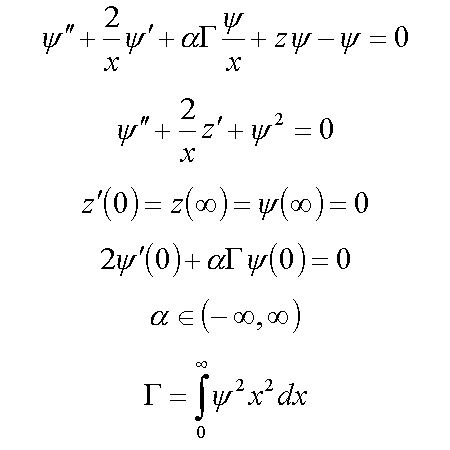
5. Polaronic condenson ( 4* )
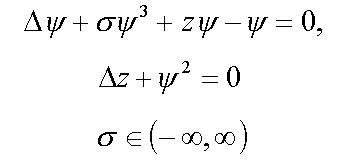
6. Bound polaronic condenson ( 4* )
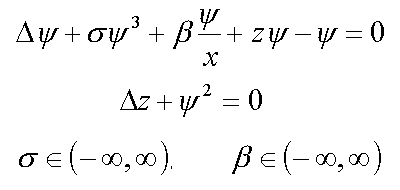
7. Electron in disordered medium with ( 1* )
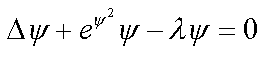
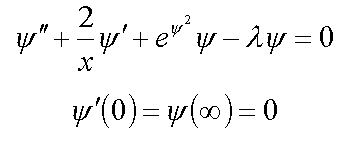
8. Electron in disordered medium with repulsoin potential ( 1* )
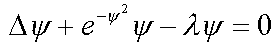
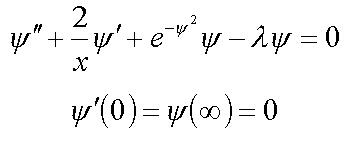
9. Continuum exciton
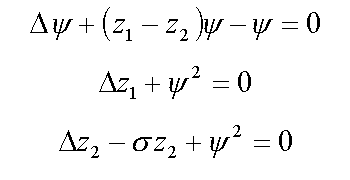
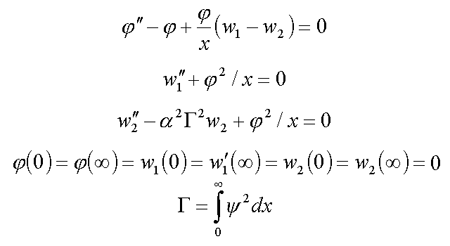
10. Continuum biexciton
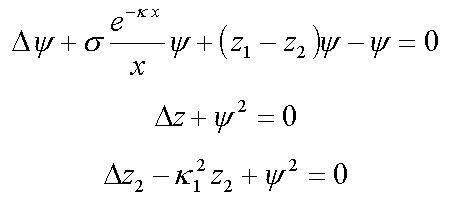
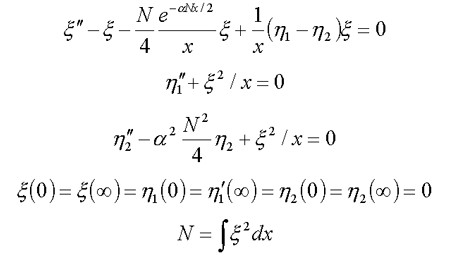
11. Solvated electron
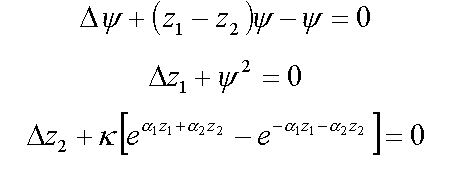
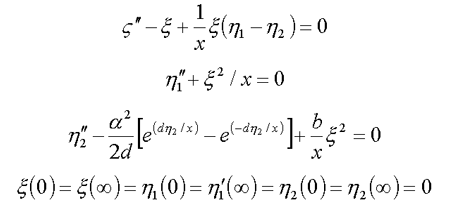
12. Nucleon in scalar meson field
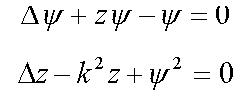
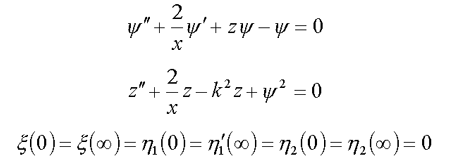
12.3. Spherically-symmetric solutions for nucleon in the nucleus ( /15/ )
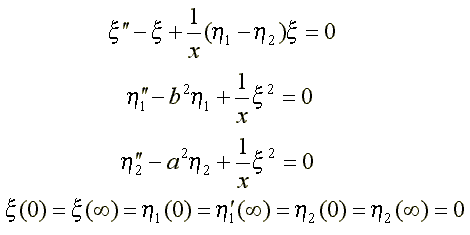
13. Bipolaronic exciton
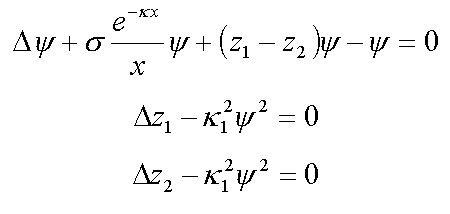
14. Nonlinear equations of electron extended ststes in proteins
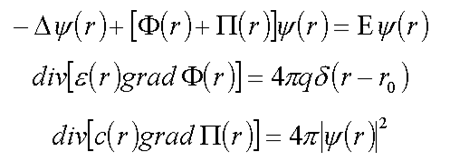
15. Equationa for particles in a quantum field at arbitrary strength of coupling ( /7/ )
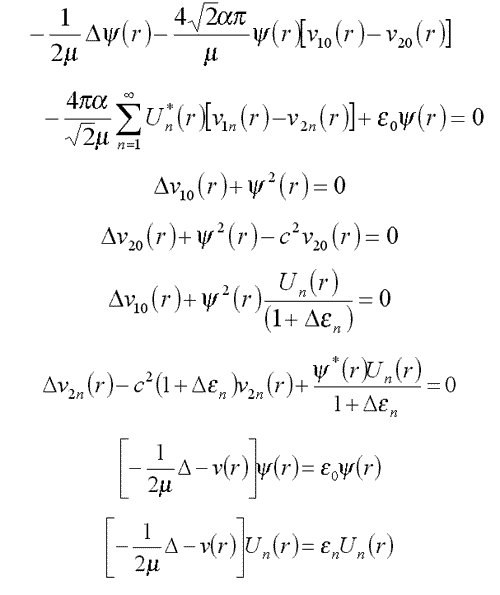
16. Equations for fluctuons
16.1. General case
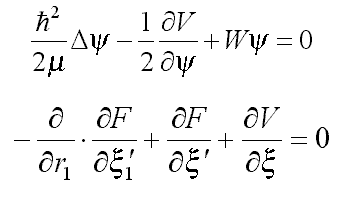
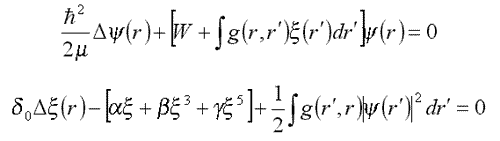
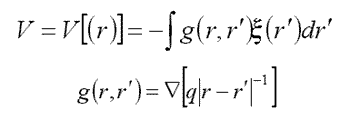
F[x]=ax2 leads to the equation for deuteron (12.1).
16.3. Krivoglaz fluctuon
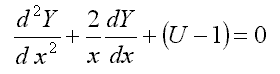
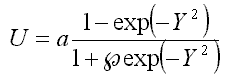
17. Discrete models
17.1. Electron in DNA ( /16/, /18/ )
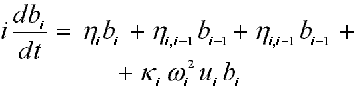
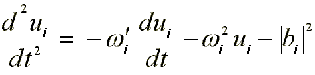
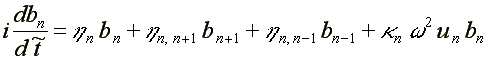
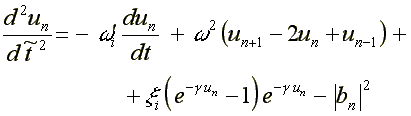
where:
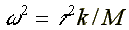 17.2. Electron in the photoreaction center of the photosyntesis ( /17/, /19/ )
17.2. Electron in the photoreaction center of the photosyntesis ( /17/, /19/ )
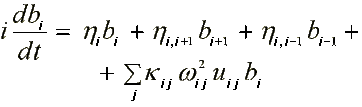
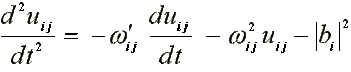
1* – R.Friedberg, J.M.Luttinger. Density of electornic levels in disordered systems //Phys. Rev. B., 1975, v.12, №10, p.4460-4474
2* – J.Wisem. Nonlinear waves. – Moscow : Mir, 1977 ( in Russian )
3* – G.L.Alfimov, V.M.Eleonsky, N.E.Kulagin, L.M.Lerman, V.P.Silin. Two-dimensional self-localized solutions of the equation Du-u+u3=0 : Preprint №238. – Moscow : Physical Institute of the USSR Academy of Sciences, 1988, p.27 ( in Russian )
4* – A.S.Davydov. Solid state theory. – Moscow : Nauka, 1976 ( in Russian )
5* – K.A.Gorshkov, V.A.Mironov, A.M.Sergeev. Nonlinear waves, self-organization. – Moscow : Nauka, 1983, с.112-128 ( in Russian )
6* – I.M.Livshits, S.A.Gredeskul, L.A.Pastur. Introduction into the theory of disordered systems. – Moscow : Nauka, 1982 ( in Russian )
7* – I.V.Amirkhanov, I.V.Puzynin, T.P.Puzynina, E.V.Zemljanaja. Iteration Method for Solving the Spherical Non-symmetrical Polaron Equation (The Luttinger LU Model) // Polarons & Applications / Ed. V.D.Lakhno. – Leeds: J.Wiley & Sons Ltd, 1994, p.445-453