Bipolarons
Review of the studies carried out
A bipolaron presents two bound polarons and may be formed in ionic crystals, liquids, semiconductors and disordered media. In /4/ and /11/ , the exact solution of the bipolaron problem was found for ionic crystals, when the interaction of two electrons with a phonon field is described by the Pekar-Frohlich Hamiltonian :
| (10.1) | 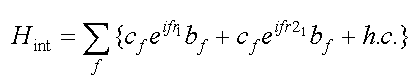 |
Here r1 and r2 are the coordinates of the first and the second electrons, respectively.
The semiphenomenological bipolaron theory assumes that in the adiabatic limit both the electrons move in the same polaron potential well, induced by their fast oscillations in this well [6*]. For this reason the electron-polarization interaction is written as :
| (10.2) | F(r1, r2) = F(r1) + F(r2) |
This form posses no translation invariancy and corresponds to the phenomenological approach, where the polarization potential well is assumed to be fixed in space. In /4/ and /11/ a consistent adiabatic translation-invariant bipolaron theory is developed, based on the Bogolubov-Tyablikov adiabatic theory. According to this approach the bipolaron movements are divided in the adiabatic limit. Relative electron coordinates describe fast electron oscillations in the potential well, which has the form of their efficient interaction :
| (10.3) | F(r1, r2) = F(r1 – r2) |
and the coordinates of the electron center mass describe slow electron motions. In this case the polarization well is not spatially fixed, but follows adiabatically the movement of the electron center mass. Interaction (10.3) is automatically translation-invariant. Fig.1 shows particle-like solutions to the bipolaron nonlinear equations (Eqs.(4.1), Sect. “Nonlinear equations of nonrelativistic quantum mechanics”). ). These solutions yield the value of the ion coupling critical parameter h=0.31, where h=e╔/e0; , e╔, e0 are high- frequency and static dielectric permittivities of the ionic crystal. The results obtained for a three-dimensional polaron are also valid for a bipolaron in two-dimensional space. The 2D-bipolaron energy and critical values of electron-phonon coupling constants at which bipolaron states are stable were also found.
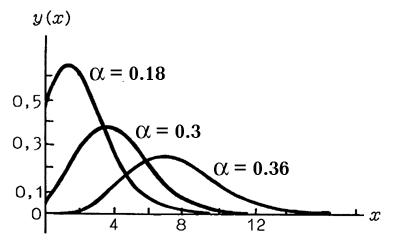
Fig.1. Particle-like solutions to bipolaron equation
for bipolaron for different values of parameter a
In /1/ and “Excited polaron states in condensed media” we considered the possibility of bipolaron states in superionic semiconductors. The estimate of the superconducting transition temperature Тc is obtained in the bipolaron superconductivity model. In particular, correct dependence of Тc on stoichiometry on oxygen x was found for the high-temperature superconductor YBa2Cu3O6+x. The possibility of the formation of bipolaron states in dopped semiconductors was analyzed in /6/ and “Polarons & Applications”.