Electron states in disordered media
Calculation of electron states in disordered media requires finding of the statistical sum
| (8.1) | 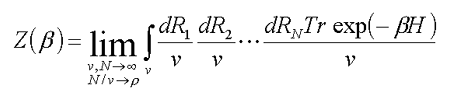 |
where
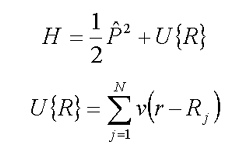
The main problem in calculation of statistical sum (8.1) is a great dimensionality of integration, which makes difficult numerical calculations for real systems, even by a supercomputer. To avoid this we can make a reduced description of the disordered system by correlation functions. For such functions we can take correlation functions of the medium density. These functions have been much studied for a wide range of media – liquids, spin glasses, polymer melts and polymer globules. Proceeding from the self-consistency of the medium and the electron states, the electron wave function can be expressed by a nonlinear differential equation of Schrodinger type with the effective potential V(f,w,Х1,Х2,…) depending on the wave function f, pairwise interaction potential V and correlation functions of the medium Х1,Х2,… :
| (8.2) | 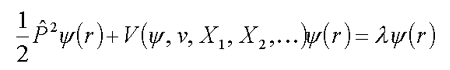 |
This equation allows to calculate electron states in complex medium taking into account the medium’s molecular structure and the thermodynamic state of the medium. The electron states in polar medium are, in essence, similar to polaron. Presently a theory is being developed, allowing to calculate the effective potential, the absorption spectrum, the effective mass and the mobility for polaron-like states in disordered medium.
When the interaction forces are polar and the medium is homogeneous this equation is reduced to the equation of the type of (3.2). In the case of short-range potential and homogeneous medium v(r-R)=2pas(r-R) the minimization of free energy corresponding to statistical sum (8.1) leads to the differential equation of the form (R.Friedberg, J.M.Luttinger. Density of electornic levels in disordered systems //Phys. Rev. B., 1975, v.12, №10, p.4460-4474) :
| (8.3) | 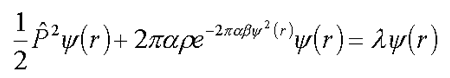 |
For a<о (Attracting potential) equation (8.3) has non-trivial solutions. Fig.1 shows the dependence of l on fo ( /2/ , see also (7.1) in “Numerical methods for solution of nonlinear boundary problems in the polaron theory”):
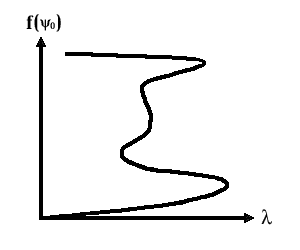
Fig.1. Where f(y0)=[ln(1+y20)]1/2, y0=y(0)
The shape of the curve suggests that there exists a region of parameter values, at which six different ground states without nodes coexist at a time. These results witness to unusual properties of nonlinear equations of quantum mechanics.